Creadores

UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TACHIRA

VICE RECTORADO ACADEMICO

DECANATO DE DOCENCIA

DEPARTAMENTO DE MATEMATICA

MATEMATICA  I

Funciones Racionales

Creado por:

Acevedo Jesús

Porras Jivirdiam

Villarroel Kevin

Zambrano Anamelia

Matematica I

San cristobal marzo de 2011

EJERCICIOS FUNCIONES RACIONALES

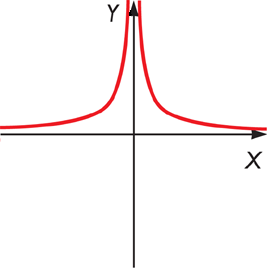
1.  

T(x) = x+2                 
          x-3

Dom T:  R - {3}

  corte con los ejes

eje y:    si x=0  →  T(0) = 0+2     →   T(0) =  2/-3
                                      0-3                      

              (0, -2/3)

eje x:   si y=0  →  x+2   = 0
                            x-3

           es decir    x+2 = 0
                            x = -2

           (-2, 0)

Asintotas:

Verticales:  el denominador se hace cero si :  x-3 = 0  →  x = 3
                    por tanto x = 3 es asintota vertical de la funcion T(x)   

Horizontales: como ambos polinomios son del mismo grado, entonces la recta y = 1/1= 1

                       y = 1 es asintota horizontal  

 

Rgo T:  R - {1}

2.         

F(x) =      x²  

             x²-9 

 F(x) =         x²                              

            (x-3)(x+3)

            

Dom F:  R - {-3,3}

cortes con los ejes

eje y:  si x = 0 →  F(0) =      0²             →  F(0) = 0

                                      (0-3)(0+3) 

   (0,0) 

eje x:   si y = 0   →          x²       = 0

                                (x-3)(x+3)

                               es decir x² = 0

                                            x = 0

   (0,0)

Asintotas:

Verticales:  x = -3  y   x = 3  ya que el denominador se hace cero

Horizontales: la recta y = 1

Rgo F: (-∞,0] U (1,∞)

3.

F(x) =    2    
           (x-3)²

Dom F: R - {3}

cortes con los ejes:

eje y:  si x = 0 →  F(0) =   2         →  F(0) = 2/9
                                      (-3)²

            (0, 2/9)

eje x: no tiene corte con el eje x

Asíntotas:

Verticales:  x = 3   presenta una desplazamiento horizontal

Horizontales: como el grado del polinomio del numerador es menor que el del denominador, entonces la recta y = 0  es asíntota horizontal.

aplicando criterios de traficación:

F(x) = 1
         x²

F(x) =   2  
          (x-3)²  

Rgo F: (0, + ∞)



4.

F(x) =    1      + 2
            x-1

Dom F: R - {1}

cortes con los ejes:

eje y:  si x = 0 →  F(0) =   1     + 2       →     F(0) = -1+2      →     F(0) = 1

                                      0-1

(0,1)

eje x:  si y = 0   →     1     + 2  = 0

                               x-1

                              1   = -2

                            x-1 

                            1 = -2x + 2     →   x = 1/2

(1/2, 0)

Asíntotas:

Verticales:  x = 1   presenta una desplazamiento horizontal


Horizontales: y = 2 es asintota horizontal ademas la grafica presenta un desplazamiento vertical

criterios de graficacion: 


F(x) =  1 
           x 

F(x) =   1  
           x-1

F(x) =   1     +  2 
           x-1

Rgo F:  R - {2}

 

5. 

F(x) = - ( 4  + 2)
              x²

Dom F: R -{0}

cortes con los ejes:
eje y: no tiene cortes
si y = 0 → _  4  - 2 = 0
                     x²
   
                     4  = -2   →     4 = - 2x²     →    x² = -2
                     x²  

 no tiene cortes con el eje x 


Asíntotas:

Verticales: el eje y es asintota vertical de la funcion (x = 0)


Horizontales: la recta y = -2

F(x) = 4
         x²

 

F(x) =  4 

           x²

 F(x) = - ( 4 + 2)

              x²

Rgo F: (- ∞, -2 )

6. 

F(x) =  3    - 2
          2-x
         
Dom F:  R - {2}

cortes con los ejes:

si x = 0  → F(0) =  3    - 2                              
                           2-0

                  F(0) = 3 -2
                            2
                  F(0) = - 1/2
                         
 (0, -1/2)

si y = 0 →  3   - 2  = 0
                 2-x

                  3     = 2
                 2-x

                3 = (4 -2x)   →    2x = 4-3    →   2x = 1    →    x = 1/2

 (1/2, 0)

Asíntotas:

Verticales:  la recta x = 2

Horizontales: la recta y = -2

F(x) =  3
           x

F(x) =  3 
          2-x

F(x) =   3      -  2
           2-x

Rgo F: (- ∞, -2) U (-2, +∞)


7.

F(x) =       8x²       
           4x² + 8x - 5

F(x) =        8x²      
           (2x-1)(2x+5) 


Dom F: R - {-5/2 , 1/2}

cortes con los ejes:

eje y : si x = 0 →   F(0) =          0²        
                                        4(0) + 8(0) -5

                             F(0) = 0


  (0,0)


eje x:  si y = 0  →        8x²         = 0

                              4x² + 8x - 5

                             es decir si y solo si  8x² = 0
                                                             x = 0


   (0,0)

Asíntotas:

Verticales: las rectas x = -5/2 y x = 1/2

Horizontales: como los polinomios son del mismo grado, entonces la recta  y = 2 , es asintota horizontal

Rgo F: (- ∞, 0] U (2,+ ∞)

8.

F(x) =  |  1    -  1|

           | x+2      |

Dom F: R -{-2}

cortes con los ejes:

eje y:   si x = 0  →   F(0) = | 1/2 -1 |   → | -1/2 | = 1/2

 (0, 1/2)

eje x: si y = 0   → |  1    -  1|    = 0     

                           | x+2      | 

                             1   -  1 = 0   

                           x+2

                         

                              1   = 1  →  1 = x+2  → x = -1

                            x+2

  (-1,0)

 Asíntotas:

Verticales: la recta x = -2

Horizontales: la recta y = 1

F(x) =  1/x

F(x) =   1  

          x+2

F(x) =   1     - 1

          x+2

 

F(x) = |  1    - 1 |

          | x+2      |

Rgo F : [0, + ∞)

9.

F(x) = -   2    

             (x+2) 

Dom F:  R - {-2}

cortes con los ejes:

eje y:   si x = 0  →   F(0) =   -     2  

                                              (0+2)

                               F(0) = -  2/8    →  - 1/4

(0, - 1/4)

eje x : si y = 0  →  -    2      = 0    

                               (x+2) 

no tiene corte con el eje x

 Asíntotas:

Verticales: la recta x = -2

 Horizontales: la recta y = 0 

F(x) =  1

           x³

F(x) =    2  

          (x+2)³

F(x) =  -     2   

               (x+2)³

 

Rgo F :  (- ∞, 0) U (0,+ ∞)

10.

F(x) =       1       -  3

            (x+2)⁴  

Dom F : R - {-2}

cortes con los ejes:

eje y:   si x = 0  →   F(0) =    1    - 3

                                        (0+2)⁴

                                F(0) = 1/16 - 3 =    -  47/16

 (0, - 47/16)

eje x : si y = 0   →   1       -  3

                            (x+2)⁴

                                1        =  3

                             (x+2)⁴

                           1 = 3 (x+2)⁴     
          

                           (x+2)⁴   =  1/3

                           x+2 =   +  ⁴√1/3

                           x =    1   - 2

                                  ⁴√3

   ( -2 + 1/ ⁴√3 ,   0)     y    (-2- ⁴√3,  0)

 Asíntotas:

Verticales: la recta x = -2

 Horizontales: la recta y =-3


F(x) =  1
          x⁴

F(x) =      1   
            (x+2)⁴

F(x) =     1       - 3
            (x+2)⁴

Rgo F: (-3 , +∞)     

          

11.

F(x) =  x² - 9
           2x - 4

Dom F: R - {2}

cortes con los ejes:

eje y:   si x = 0  →   F(0) =   0² - 9
                                         2(0) - 4

                                F(0) = - 9/-4  =  9/4

 (0, 9/4)

eje x:   si y = 0  →   x² - 9      = 0
                               2x- 4

                                (x-3)(x+3)      = 0
                                    2x-4

                                 si x = 3 ó x = -3  entonces la fraccion se anula (3,0) ; (-3, 0)


Asíntotas:

Verticales: la recta x = 2

 Oblicuas:  como el grado del polinomio del numerador es mayor en uno que el del denominador entonces hay asintotas oblicuas  y es la recta y = ax + b. Para ello realizamos:

  x² - 9                |2x - 4
 -x² - + 2x            1/2 x + 1
            2x  - 9
           -2x +4
                 - 5

 x² - 9   =     (1/2x + 1) -    _5    
 2x- 4                               2x - 4

por lo tanto y = 1/2 x +1  es A.O

Rgo F:  [1, +  ∞)

Funciones Racionales

Una función racional es una función de la forma

f(x) = p(x)
         q(x)

Donde p(x) y q(x) son polinomios y q (x) ≠ 0

A diferencia de una función polinomial, cuyo dominio es siempre el conjunto de todos los numeros reales, una funcion racional puede tener un dominio restringido, ya q se debe excluir cualquier valpr que anule al denominador.

Un caso particular que merece especial atencion es el de las funciones de las formas

f(x) = 1  , para enteros positivos n ≥ 1
        xⁿ

                                                                y = 1  , para n impar
                                                                     xⁿ

                                                                 y = 1  , para n par
                                                                      xⁿ


Ambas graficas tienen como asintota vertical a x=0 y como asintota horizontal a y=0

En general puede afirmarse q para x ∈ R - {0}, el comportamiento de las funciones y= 1/xⁿ    y   y = 1/xº
                                                                                                                                 
con n y o enteros positivos, o   1 y n  ≥ 1, ofrece las siguientes caracteristicas:


a) En el caso de q n y o sean pares, y n <  o

                                       |x| ≥ 1, xº ≤ xⁿ
                                     
                                       |x|  < 1, xº > xⁿ


b)  En el caso de q n y o sean impares, y n <  o


                                      |x| ≥ 1,| xº| ≤ |xⁿ|
                                     
                                       |x|< 1,| xº| > |xⁿ|


En el estudio de las funciones racionales tiene particular importancia el analizis de las asistontas verticales y horizontales.

Definicion de asintota vertical:

La recta x=a es asintota vertical de la grafica de una funcion f si f(x) → ∞  bien  f(x) → -∞  cuando x→a , por la izquierda o por la derecha.

Definicion de asintota horizontal:

la recta y=c es asintota horizontal de la grafica de una funcion f si   f(x) → c cuando x → ∞ o cuando x → -∞  

Nota:
Para determinar las asintotas verticales, se acostumbra obtener los ceros del denominador, si embargo si a es un cero del denominador de una funcion racional f, entonces la grafica de f puede tener una asintota vertical x=a, pues hay funciones racionales para las cuales este no es el caso.

Con mayor precision puede afirmarse que si tanto el numerador como el denominador no tienen factor comun, entonces f debe tener una asintota vertical x=a, en otras palabras, para que x=a sea asintota vertical debe ser un cero del denominador pero no debe anular el numerador.

La grafica de una funcion racional puede no tener asintotas horizontales, y en caso de tenenerla la grafica puede cruzar dicha asintota.